NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5
Ex 1.5 Class 9 Maths Question 1.
Classify the following numbers as rational or irrational:
(1) 2-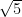
(2) (3+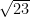 )-
)-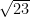
(3)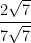
(4)
(5) 2π
Solution:(1) Irrational ∵ 2 is a rational number and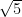 is an irrational number.
is an irrational number.
∴ 2 –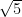 is an irrational number.
is an irrational number.
(∵ The difference of a rational number and an irrational number is irrational)
Classify the following numbers as rational or irrational:
(1) 2-
(2) (3+
(3)
(4)
(5) 2π
Solution:(1) Irrational ∵ 2 is a rational number and
∴ 2 –
(∵ The difference of a rational number and an irrational number is irrational)
(2) 3 + 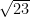 –
– 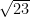 = 3 (rational)
= 3 (rational)
(3) 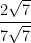 =
= (rational)
(rational)
(4) 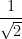 (irrational) ∵ 1 ≠ 0 is a rational number and
(irrational) ∵ 1 ≠ 0 is a rational number and  2 ≠ 0 is an irrational a/2 number.
2 ≠ 0 is an irrational a/2 number.
∴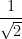 = is an irrational number.
= is an irrational number.
(∵ The quotient of a non-zero rational number with an irrational number is irrational).
(5) 2π (irrational) ∵ 2 is a rational number and π is an irrational number.
∴ 2π is an irrational number, (∵ The product of a non-zero rational number with an irrational number is an irrational).
∴
(∵ The quotient of a non-zero rational number with an irrational number is irrational).
(5) 2π (irrational) ∵ 2 is a rational number and π is an irrational number.
∴ 2π is an irrational number, (∵ The product of a non-zero rational number with an irrational number is an irrational).
Ex 1.5 Class 9 Maths Question 2.
Simplify each of the following expressions :(1) (3 + ) (2 + a/2)
) (2 + a/2)
(2) (3 + ) (3-
) (3- )
)
(3) (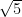 +
+  )2
)2
(4) (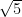 –
–  ) (
) (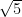 +
+  )
)
Solution:

Simplify each of the following expressions :(1) (3 +
(2) (3 +
(3) (
(4) (
Solution:

Ex 1.5 Class 9 Maths Question 3.
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is
π = . This seems to contradict the fact that it is irrational. How will you resolve this contradiction?
. This seems to contradict the fact that it is irrational. How will you resolve this contradiction?
Solution:
Actually =
=  which is an approximate value of π.
which is an approximate value of π.
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is
π =
Solution:
Actually
Ex 1.5 Class 9 Maths Question 4.
Represent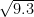 on the number line.
on the number line.
Solution:
Mark the distance 9.3 units from a fixed point A on a given line to obtain a point B such that AB = 9.3 units. From B, mark a distance of 1 unit and mark the new point as C. Find the mid-point of AC and mark that point as O. Draw a semi-circle with center O and radius OC. Draw a line perpendicular to AC passing through B and intersecting the semi-circle at D

Then BD =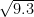 . To represent
. To represent 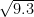 on the number line. Let us treat the line BC as the number line, with B as zero, C as 1, and so on. Draw an arc with center B and radius BD, which intersects the number line at point E. Then, the point E represent
on the number line. Let us treat the line BC as the number line, with B as zero, C as 1, and so on. Draw an arc with center B and radius BD, which intersects the number line at point E. Then, the point E represent 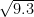 .
.
Represent
Solution:
Mark the distance 9.3 units from a fixed point A on a given line to obtain a point B such that AB = 9.3 units. From B, mark a distance of 1 unit and mark the new point as C. Find the mid-point of AC and mark that point as O. Draw a semi-circle with center O and radius OC. Draw a line perpendicular to AC passing through B and intersecting the semi-circle at D

Then BD =
Ex 1.5 Class 9 Maths Question 5.
Rationalise the denominators of the following:
(i)
(ii)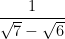
(iii)
(iv)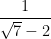
Solution:

Rationalise the denominators of the following:
(i)
(ii)
(iii)
(iv)
Solution:








0 comments:
Post a Comment
THANK YOU