NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3
Ex 1.3 Class 10 Maths Question 1.Prove that √5 is irrational.
Solution:Let √5 = be a rational number, where p and q are co-primes and q ≠ 0.
be a rational number, where p and q are co-primes and q ≠ 0.
Then, √5q = p => 5q2=p2⇒ p2 – Sq2 … (i)
Since 5 divides p2, so it will divide p also.
Let p = 5r
Then p2 – 25r 2 [Squaring both sides]
⇒ 5q2 = 25r2 [From(i)]
⇒ q2 = 5r2Since 5 divides q2, so it will divide q also. Thus, 5 is a common factor of both p and q.
This contradicts our assumption that √5 is rational.
Hence, √5 is irrational. Hence, proved.
Solution:Let √5 =
Then, √5q = p => 5q2=p2⇒ p2 – Sq2 … (i)
Since 5 divides p2, so it will divide p also.
Let p = 5r
Then p2 – 25r 2 [Squaring both sides]
⇒ 5q2 = 25r2 [From(i)]
⇒ q2 = 5r2Since 5 divides q2, so it will divide q also. Thus, 5 is a common factor of both p and q.
This contradicts our assumption that √5 is rational.
Hence, √5 is irrational. Hence, proved.
Ex 1.3 Class 10 Maths Question 2.
Show that 3 + √5 is irrational.
Solution:Let 3 + 2√5 = be a rational number, where p and q are co-prime and q ≠ 0.
be a rational number, where p and q are co-prime and q ≠ 0.
Then, 2√5 = – 3 =
– 3 = 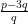
⇒ √5 =
since is a rational number,
is a rational number,
therefore, √5 is a rational number. But, it is a contradiction.
Hence, 3 + √5 is irrational. Hence, proved.
Show that 3 + √5 is irrational.
Solution:Let 3 + 2√5 =
Then, 2√5 =
⇒ √5 =
since
therefore, √5 is a rational number. But, it is a contradiction.
Hence, 3 + √5 is irrational. Hence, proved.
Ex 1.3 Class 10 Maths Question 3.Prove that the following are irrational.

Solution:
(i) Let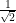 =
=  be a rational number,
be a rational number,
where p and q are co-prime and q ≠ 0.
Then, √2 =
Since is rational, therefore, √2 is rational.
is rational, therefore, √2 is rational.
But, it is a contradiction that √2 is rational, rather it is irrational.
Hence,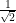 is irrational.
is irrational.
Hence, proved.

Solution:
(i) Let
where p and q are co-prime and q ≠ 0.
Then, √2 =
Since
But, it is a contradiction that √2 is rational, rather it is irrational.
Hence,
Hence, proved.
(ii) Let 7√5 =  be a rational number, where p, q are co-primes and q ≠ 0.
be a rational number, where p, q are co-primes and q ≠ 0.
Then, √5 =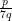
Since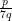 is rational therefore, √5 is rational.
is rational therefore, √5 is rational.
But, it is a contradiction that √5 is rational rather it is irrational.
Hence, 7√5 s is irrational.
Hence proved.
Then, √5 =
Since
But, it is a contradiction that √5 is rational rather it is irrational.
Hence, 7√5 s is irrational.
Hence proved.
(iii) Let 6 + √2 =  be a rational number, where p, q are co-primes and q ≠ 0.
be a rational number, where p, q are co-primes and q ≠ 0.
Then, √2 = – 6 =
– 6 = 
Since is rational therefore, √2 is rational.
is rational therefore, √2 is rational.
But, it is a contradiction that √2 is rational, rather it is irrational.
Hence, 6 + √2 is irrational.
Then, √2 =
Since
But, it is a contradiction that √2 is rational, rather it is irrational.
Hence, 6 + √2 is irrational.










0 comments:
Post a Comment
THANK YOU