NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4

Ex 1.4 Class 9 Maths Question 1.
Visualize 3.765 on the number line, using successive magnification.
Solution:
We know that 3.765 lies between 3 and 4. So, let us divide the part of the number line between 3 and 4 into 10 equal parts and look at the portion between 3.7 and 3.8 through a magnifying glass. Now 3.765 lies between 3.7 and 3.8 [Fig. (i)]. Now, we imagine dividing this again into ten equal parts. The first mark will represent 3.71, the next 3.72 and so on. To see this clearly, we magnify this as shown in
[Fig. (ii)].

Again 3.765 lies between 3.76 and 3.77 [Fig. (ii)]. So, let us focus on this portion of the number line [Fig. (iii)] and imagine to divide it again into ten equal parts [Fig. (iii)]. Here, we can visualize that 3.761 is the first mark and 3.765 is the 5th mark in these subdivisions. We call this process of visualization of representation of numbers on the number line through a magnifying glass as the process of successive magnification. So, we get seen that it is possible by sufficient successive magnifications of visualizing the position (or representation) of a real number with a terminating decimal expansion on the number line

Ex 1.4 Class 9 Maths Question 2.
Visualise  on the number line, upto 4 decimal places.
Solution:
We adopt a process by successive magnification and successively decrease the lengths of the portion of the number line in which  is located. Since  is located between 4 and 5 and is divided into 10 equal parts [Fig. (i)]. In further, we locate  between 4.2 and 4.3 [Fig. (ii)].

To get more accurate visualization of the representation, we divide this portion into 10 equal parts and use a magnifying glass to visualize that  lies between 4.26 and 4.27. To visualise  more clearly we divide again between 4.26_and 4.27 into 10 equal parts and visualise the representation of  between 4.262 and 4.263 [Fig. (iii)].

Now, for a much better visualization between 4.262 and 4.263 is again divided into 10 equal parts
[Fig. (iv)]. Notice that  is located closer to 4.263 then to 4.262 at 4.2627.

Remark: We can adopt the process endlessly in this manner and simultaneously imagining the decrease in the length of the number line in which 4.26 is located.

Read More

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3

Ex 1.3 Class 9 Maths Question 1.
Write the following in decimal form and say what kind of decimal expansion each has :(1) 
(2) 
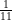
(3) 4
(4) 
(5) 
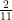
(6) 
Solution:
(1)   = 0.36, terminating.
(2) By long division, we have

(3)

(4)

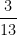∴  = 0.23076923 = 
(5)

∴  = 0.181818 = 

(6)

Ex 1.3 Class 9 Maths Question 2.
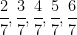
You know that  =  .Can you predict what the decimal expansions of  are, without actually doing the long  division? If so, how? [Hint: Study the remainders while finding the value of  carefully.]
Solution:
We have, = 

Ex 1.3 Class 9 Maths Question 3.
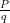
Express the following in the form , where p and q are integers and q ≠ 0.

1. 
2. 0.
3.   

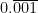
Solution:
(1) Let x =  = 0.666…………     …(i)
Multiplying Eq. (i) by 10, we get
10x = 6.666…                 …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
(10x – x) = (6.666…) – (0.666…)
9x = 6 => x = 6/9           => x = 2/3
x = 0.  = 0.4777

(2) Let
Multiplying Eq. (i) by 10, we get
10x = 4.777…                       …(ii)
Multiplying Eq. (ii) by 10, we get
100x = 47.777                                               … (iii)
On subtracting Eq. (ii) from Eq. (iii), we get
(100x-10x)= (47.777…) – (4.777…)
90x =43      => x = 
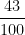
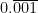
x =  = 0.001001001…

(3) Let
Multiplying Eq. (i) by 1000, we get
1000x = 1.001001001…
On subtracting Eq. (i) from Eq. (ii), we get
(1000x – x) = (1.001001001…) – (0.001001001…)
999x = 1  => 

Ex 1.3 Class 9 Maths Question 4.
Express 0.99999… in the form . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Let x = 0.9999…                                                                              …(i)
Here, we have only one repeating digit. So, we multiply both sides of (i) by 10 to get

10x = 9.999….                                        …(ii)
Subtracting (i) from,(ii), we get
10x-x = (9.999…)-(0.9999…)
=>   9x = 9
=> x = 1
Hence, 0.9999…= 1
Since, 0.9999… goes on forever. So, there is no gap between 1 and 0.9999… and hence they are equal.

Ex 1.3 Class 9 Maths Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion ? Perform the division to check your answer.
Solution:

Ex 1.3 Class 9 Maths Question 6.
Look at several examples of rational numbers in the form  (q ≠ 0), where, p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Consider many rational numbers in the form  (q ≠ 0) , where p and q are
integers with no common factors other than 1 and having terminating decimal representations.



From the above, we find that the decimal expansion of the above numbers is terminating. Along with we see that the denominator of the above numbers are in the form 2m x 5n, where m and n are natural numbers. So, the decimal representation of rational numbers can be represented as a terminating decimal.

Ex 1.3 Class 9 Maths Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
Three numbers whose decimal representations are non-terminating and non-repeating are
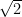
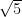
 , and  or we can say 0.100100010001…, 0.20200200020002… and 0.003000300003…

Ex 1.3 Class 9 Maths Question 8.
Find three different irrational numbers between the rational numbers and .
Solution:
To find irrational numbers, firstly we shall divide 5 by 7 and 9 by 11,

Thus, = 0.8181… = 
The required numbers are
0.73073007300073000073…
0.7650765007650007650000…
0.80800800080000…

Ex 1.3 Class 9 Maths Question 9.
Classify the following numbers as rational or irrational:
(1) 
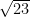
(2) 
(3) 0.3796
(4) 478478…
(5) 1.101001000100001…
Solution:
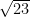
(1)   is an irrational number as 23 is not a perfect square.
(2)  

Thus, 15 is a rational number.
(3) 0.3796 is a rational number as it is terminating decimal.
(4) 7.478478… is non-terminating but repeating, so, it is a rational number.
(5) 1.101001000100001… is non-terminating and non-repeating so, it is an irrational number.

Thus, = 
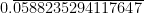
∴ The maximum number of digits in the quotient while computing  are 16.

Read More